Life is full of "What if?" questions. Math is one tool we use to answer those questions. That's a good reason to teach math to kids, and why grown-ups need to be able use that math later in their lives.
PAST TENSE
What if I had gone out with Sue instead of Laurie?
What if I had taken the first job instead of the second one? The first job paid $6 per hour plus tips but no overtime and no benefits, but the job I accepted paid $7.50 and $11.25 overtime and I accrued vacation time ... What if?
Looking back and trying to figure out what would have happened if? is a recipe for frustration. Here's one of my favorite passages on that subject, from The Lion, The Witch and the Wardrobe, by CS Lewis:
"Oh, Aslan," said Lucy. "You don't mean it ... I couldn't have left the others and come up to you alone, how could I? Don't look at me like that . . . oh well, I suppose I could ... But what would have been the good?"
Aslan said nothing.
"You mean," said Lucy rather faintly, "that it would have turned out all right - somehow? But how? Please, Aslan! Am I not to know [how it would have turned out]?"
"To know what would have happened, child?" said Aslan. "No. Nobody is ever told that."
"Oh dear," said Lucy.
"But anyone can find out what will happen ... and there is only one way of finding out..."
"Do you mean that is what you want me to do?" gasped Lucy.
"Yes, little one," said Aslan.
"Will the others see you too?" asked Lucy.
"Certainly not at first," said Aslan. "Later on, it depends."
"But they won't believe me!" said Lucy.
"It doesn't matter," said Aslan.
Lewis suggests here and in other places that we can't know what would have happened. But we can look back at what did happen, and try to make sense of it. Defining the past in ways that make sense is often called History.
You can’t connect the dots looking forward; you can only connect
them looking backwards. So you have to trust that the dots will somehow
connect in your future.
I like this statement made by Steve Jobs - I have seen it repeated many times since he died.
On the one hand, history teaches us a great deal. IF we listen. We often do not.
On the other hand, history does not predict the future, as any stock broker will tell you! Or rather, they will say "past performance is not an indicator of future results."
I predict that tomorrow this blog will deal with the question of future predictions.
Friday, October 28, 2011
Reckoning on Ratios
Ratio: A quantitative relation between two amounts; the number of times one value contains or is contained within the other value.
In English, the origin of ratio dates back to about 1636, coming from Latin and meaning "reason, rationale, reckoning, calculation, procedure, or think." It's been used in a mathematical sense since 1660.
For example, my garage contains 2 red cars and my driveway contains 4 blue cars, so the ratio of red cars to blue cars is 2 to 4, also written 2:4. A ratio can also be expressed as a decimal or percentage.
I provided examples of ratios in the past two blogs: Power to Weight, and Height to Width.
Today I want to show how in bread, the key ratio is water to flour, by weight. I'm not going to use volume for the measurements, and you will soon see why.
Here's some water. One pound; or 16 ounces; or 450 grams by weight.
Yeast goes in next. It doesn't really weigh anything, as I use only a quarter-teaspoon.
Now I add a bunch of flour.
One and one quarter pounds; or 20 ounces; or 560 grams by weight.
Our ratio is 16 water to 20 flour, which we can simplify to 4 water to 5 flour or 4:5.
I'm a little overweight here on the flour. I will take 3/8 ounce out before I add a bit less than one tablespoon of kosher salt.
When the yeasts start to eat up the complex carbohydrates in the flour they give off gas. It makes the batter start to expand and rise. Here we have one quart by volume, but the ratio by weight is still the same.
They keep eating and the dough keeps rising. Here we have three quarts by volume, but the ratio by weight is still the same! The dough is less dense, but we have the same weight.
Now it comes out onto the table and is dusted with a tiny bit of flour so it won't be sticky. I shape it into a ball. The ratio is still the same - 4 water and 5 flour.
The dough goes into a hot cast iron pan in my oven. It keeps rising. The volume has increased a great deal since we put the water and flour together with yeast and salt.
Here's the final loaf after it comes out of the oven. We have added water, flour, yeast, salt, time and temperature. The volume has increased. Is the ratio of water to flour still the same? Yes or No?
Sorry. The answer is no. When you bake the bread lots of the water evaporates. By my measuring, about 20% of the weight of the water is gone, so the bread weighs 2 pounds, instead of 2 pounds 4 ounces. The ratio is now 4 to 4 or simplified - it's 1:1.
And it's time for my lunch!
In English, the origin of ratio dates back to about 1636, coming from Latin and meaning "reason, rationale, reckoning, calculation, procedure, or think." It's been used in a mathematical sense since 1660.
For example, my garage contains 2 red cars and my driveway contains 4 blue cars, so the ratio of red cars to blue cars is 2 to 4, also written 2:4. A ratio can also be expressed as a decimal or percentage.
I provided examples of ratios in the past two blogs: Power to Weight, and Height to Width.
Today I want to show how in bread, the key ratio is water to flour, by weight. I'm not going to use volume for the measurements, and you will soon see why.
Here's some water. One pound; or 16 ounces; or 450 grams by weight.
Yeast goes in next. It doesn't really weigh anything, as I use only a quarter-teaspoon.
Now I add a bunch of flour.
One and one quarter pounds; or 20 ounces; or 560 grams by weight.
Our ratio is 16 water to 20 flour, which we can simplify to 4 water to 5 flour or 4:5.
I'm a little overweight here on the flour. I will take 3/8 ounce out before I add a bit less than one tablespoon of kosher salt.
Mix up the ingredients with a spoon and it looks like this.
When the yeasts start to eat up the complex carbohydrates in the flour they give off gas. It makes the batter start to expand and rise. Here we have one quart by volume, but the ratio by weight is still the same.
They keep eating and the dough keeps rising. Here we have three quarts by volume, but the ratio by weight is still the same! The dough is less dense, but we have the same weight.
Now it comes out onto the table and is dusted with a tiny bit of flour so it won't be sticky. I shape it into a ball. The ratio is still the same - 4 water and 5 flour.
The dough goes into a hot cast iron pan in my oven. It keeps rising. The volume has increased a great deal since we put the water and flour together with yeast and salt.
Here's the final loaf after it comes out of the oven. We have added water, flour, yeast, salt, time and temperature. The volume has increased. Is the ratio of water to flour still the same? Yes or No?
Sorry. The answer is no. When you bake the bread lots of the water evaporates. By my measuring, about 20% of the weight of the water is gone, so the bread weighs 2 pounds, instead of 2 pounds 4 ounces. The ratio is now 4 to 4 or simplified - it's 1:1.
And it's time for my lunch!
Thursday, October 27, 2011
Rationalizing Irksome Illustrations
My friend Susan and I were discussing how photos appear on website and advertisements. Both of us are irked when illustrations are stretched or squashed to fit in the available space. The technical term for this is "out of proportion." We cover this even in elementary school math when we discuss ratios.
Let me explain what I mean.
You might see descriptions in your camera or photo software that say 3 by 2, or 4 by 6, or 1024 by 768. In all of these cases, we are showing the width and the height of the image. In the first case the ratios have been reduced, or simplified as far as possible. In the latter case, it's the count of pixels in a horizontal direction followed by the pixels in the vertical direction.
What is 1024 by 768 simplified? We are looking for the greatest common denominator, which turns out to be 256. The ratio is 4 by 3.
Now let me show you what I mean by irksome illustrations. Here are three versions of a picture I took the other night:
The center one is at its original aspect ratio (height to width) and the other two are "squished" and "stretched" by only 10%. I left the height alone and altered the widths. These changes are quite noticeable on pictures with a round shape in the center. Our eyes are good at picking up "out of round" conditions.
Now let's try it with some faces. These talented folks are my friends and family members. They were hanging spoons on their noses during dinner, just to show me that they could. Notice the giraffe-like necks in the vertically-stretched image?
This is about the most distortion you can get away with - before viewers say Hey! What's going on!
Now let's examine one more example. Here's a Toyota Scion - yes, a boxy little car to start with, but it's worth using to make a point. In this case I took a horizontally-oriented picture and made it square. This is a common error made by people laying out ads for used cars.
In the square picture, it hardly looks like a real car. Sigh.
Folks, don't do this! Please! Lock the proportions in your layout or photo editing software, or at least stay within a few percent of the original aspect ratios. Even if we can't remember the math that explains what you have done, we will notice.
PS- yesterday we talked about pounds per horsepower; today it's height by width. Both are ratios.
Let me explain what I mean.
You might see descriptions in your camera or photo software that say 3 by 2, or 4 by 6, or 1024 by 768. In all of these cases, we are showing the width and the height of the image. In the first case the ratios have been reduced, or simplified as far as possible. In the latter case, it's the count of pixels in a horizontal direction followed by the pixels in the vertical direction.
What is 1024 by 768 simplified? We are looking for the greatest common denominator, which turns out to be 256. The ratio is 4 by 3.
Now let me show you what I mean by irksome illustrations. Here are three versions of a picture I took the other night:
The center one is at its original aspect ratio (height to width) and the other two are "squished" and "stretched" by only 10%. I left the height alone and altered the widths. These changes are quite noticeable on pictures with a round shape in the center. Our eyes are good at picking up "out of round" conditions.
Now let's try it with some faces. These talented folks are my friends and family members. They were hanging spoons on their noses during dinner, just to show me that they could. Notice the giraffe-like necks in the vertically-stretched image?
This is about the most distortion you can get away with - before viewers say Hey! What's going on!
Now let's examine one more example. Here's a Toyota Scion - yes, a boxy little car to start with, but it's worth using to make a point. In this case I took a horizontally-oriented picture and made it square. This is a common error made by people laying out ads for used cars.
In the square picture, it hardly looks like a real car. Sigh.
Folks, don't do this! Please! Lock the proportions in your layout or photo editing software, or at least stay within a few percent of the original aspect ratios. Even if we can't remember the math that explains what you have done, we will notice.
PS- yesterday we talked about pounds per horsepower; today it's height by width. Both are ratios.
Wednesday, October 26, 2011
The Rate of Change
Acceleration is a term that describes the rate of change of both the magnitude and the direction of velocity of an object.
What's this? you ask. Are we getting into physics?
Normally, this blog discusses ways that average adults like us today can use math we learned back then to deal with our everyday lives. The blog supports our goal that Excel Math (elementary math curriculum) will help prepare kids to be more confident and competent adult citizens.
A lofty goal, eh?
But today we reach even further. One of our executives challenged me to incorporate something his son learned in school last week. So here we go:
THEORY
NEWTON'S Second Law of Motion: The acceleration a of a body is parallel and directly proportional to the net force F and inversely proportional to the mass m, therefore F = ma.
And thus a = F/m which means Acceleration equals Force divided by Mass
In physics the term Acceleration is used for either increasing or decreasing in velocity, while in our normal conversation we say Acceleration to talk about an increase in velocity, and Deceleration for a decrease in velocity.
An object that's accelerating can be thrown or projected, self-powered, or falling (pulled by gravity). It can go in a straight line, or it can be rotating or orbiting.
Let's examine the formula again: Acceleration equals Force divided by Mass
In plain language, if you want to accelerate quickly, you need a powerful force (engine) or a light projectile. Or both. At this point, most men are probably thinking about cars ...
PRACTICAL EXAMPLES
Contrary to popular thought, flames don't make you go fast. This is still a golf cart and accelerates like one, despite the clever '57 Chevy styling and the flame paint job. It has between 11 horsepower for its 750 pounds, or 1 hp for every 68 pounds.
This Navy LCAC (landing craft air cushion) has lots more power - 16,000 continuous horsepower to be exact. But it weighs 100 tons with a modest load on board. Since the power is lifting as well as propelling, the acceleration is fairly feeble. It has about 1 horsepower for each 12.5 pounds of mass.
The Caterham sports car I'm driving here is an excellent accelerator! It's very light at 1130 lbs (plus me) and has 175 hp, for 1 hp to 6.5 pounds mass.
Finally, if you want to accelerate VERY VERY QUICKLY, you could try a drive in this car. It weighs about 2250 lbs and produces 8000 horsepower (for 10 seconds). The power to weight ratio is 0.28 pounds per horsepower, or 1 hp for every 4 ounces.
3 seconds!!!!!!!!!!!!!!!! - in the amount of time it took me to type just those 16 exclamation marks, this car can reach 250 mph.
PS - remember what I said earlier about flames not making your car go any faster? Well, I have since learned that the real flames (exhaust) from a dragster generate about 800–1000 pounds of push (force) to assist the car going forward.
What's this? you ask. Are we getting into physics?
Normally, this blog discusses ways that average adults like us today can use math we learned back then to deal with our everyday lives. The blog supports our goal that Excel Math (elementary math curriculum) will help prepare kids to be more confident and competent adult citizens.
A lofty goal, eh?
But today we reach even further. One of our executives challenged me to incorporate something his son learned in school last week. So here we go:
THEORY
NEWTON'S Second Law of Motion: The acceleration a of a body is parallel and directly proportional to the net force F and inversely proportional to the mass m, therefore F = ma.
And thus a = F/m which means Acceleration equals Force divided by Mass
In physics the term Acceleration is used for either increasing or decreasing in velocity, while in our normal conversation we say Acceleration to talk about an increase in velocity, and Deceleration for a decrease in velocity.
An object that's accelerating can be thrown or projected, self-powered, or falling (pulled by gravity). It can go in a straight line, or it can be rotating or orbiting.
Let's examine the formula again: Acceleration equals Force divided by Mass
In plain language, if you want to accelerate quickly, you need a powerful force (engine) or a light projectile. Or both. At this point, most men are probably thinking about cars ...
PRACTICAL EXAMPLES
Contrary to popular thought, flames don't make you go fast. This is still a golf cart and accelerates like one, despite the clever '57 Chevy styling and the flame paint job. It has between 11 horsepower for its 750 pounds, or 1 hp for every 68 pounds.
This Navy LCAC (landing craft air cushion) has lots more power - 16,000 continuous horsepower to be exact. But it weighs 100 tons with a modest load on board. Since the power is lifting as well as propelling, the acceleration is fairly feeble. It has about 1 horsepower for each 12.5 pounds of mass.
The Caterham sports car I'm driving here is an excellent accelerator! It's very light at 1130 lbs (plus me) and has 175 hp, for 1 hp to 6.5 pounds mass.
Finally, if you want to accelerate VERY VERY QUICKLY, you could try a drive in this car. It weighs about 2250 lbs and produces 8000 horsepower (for 10 seconds). The power to weight ratio is 0.28 pounds per horsepower, or 1 hp for every 4 ounces.
3 seconds!!!!!!!!!!!!!!!! - in the amount of time it took me to type just those 16 exclamation marks, this car can reach 250 mph.
PS - remember what I said earlier about flames not making your car go any faster? Well, I have since learned that the real flames (exhaust) from a dragster generate about 800–1000 pounds of push (force) to assist the car going forward.
Tuesday, October 25, 2011
Suffixed Math
Yesterday we tackled a list of prefixes, short groups of letters that begin a word. Today we'll take a similar approach to a group of suffixes - short groups of letters that end a word.
Not all of these are commonly used in mathematical calculations, but these suffixes are common in the related fields of geometry, trigonometry, the other sciences, etc. If you want to be considered brainy, you need to know what they mean.
If I want to be considered brainy, I have to remember how to build animated GIFs. I forgot yesterday so my "animated brain" was stationary rather than active.
Please read through the list carefully - can you think of other suffixes that I missed?
I think this will end my treatment of word prefixes and suffixes in the blog.
However, if you enjoyed it, go to this tremendous site. The creator says:
"Vocabulary is at the core of literacy and the more extensive our vocabulary is, the greater will be the understanding of what we read and hear."
Type a prefix or suffix into his search box, hit ENTER and then click on the result to get a list of words.
While searching around for prefixes and suffixes, I found this great math sentence:
I have nothing more to say, because my mind grows number with each additional effort, and after eating a number of peppermint candies, my mouth has gotten number too.
Not all of these are commonly used in mathematical calculations, but these suffixes are common in the related fields of geometry, trigonometry, the other sciences, etc. If you want to be considered brainy, you need to know what they mean.
Please read through the list carefully - can you think of other suffixes that I missed?
| Suffix | Meaning | Example |
| -centenary | hundred years | bicentennial (200th) |
| -gon | number of interior angles | polygon, hexagon, etc |
| -gram | line overwritten or drawn on top | hexagram, 6-pointed star |
| -graph | to draw, write or scratch | angiograph, paragraph |
| -hedral, -on | number of faces or surfaces | polyhedral, hexahedron |
| -ic | related to arts or sciences | arithmetic |
| -lateral | ahead, before in line, first in order | equilateral |
| -logy | to study; a body of knowledge | trilogy, ecology |
| -ment | action, skill or process | assessment, alignment |
| -metry | measuring | geometry, symmetry |
| -nomial | a term in a math expression or formula | polynomial |
| -oid | resembles, similar to | spheroid, cuboid, android |
| -sect | to cut, divide or connect | intersect, bisect, trisect |
| -scope | to examine or view | microscope, kaleidoscope |
| -scribe | to write | transcribe, circumscribe |
| -sphere | globe or ball | hemisphere, 3-sphere |
I think this will end my treatment of word prefixes and suffixes in the blog.
However, if you enjoyed it, go to this tremendous site. The creator says:
"Vocabulary is at the core of literacy and the more extensive our vocabulary is, the greater will be the understanding of what we read and hear."
Type a prefix or suffix into his search box, hit ENTER and then click on the result to get a list of words.
While searching around for prefixes and suffixes, I found this great math sentence:
I have nothing more to say, because my mind grows number with each additional effort, and after eating a number of peppermint candies, my mouth has gotten number too.
Monday, October 24, 2011
Pre-Fixed Math
As I begin this post on using elementary math as a grown-up, I have to warn you that despite the way the title sounds, this is is NOT about cheating on tests, pre-school math, nor is it about French meals with a fixed price.
This post is about pre-fixes, those short letter combinations that appear in front of other (math) words.
That's enough - I think you get the idea. Of course there are many more obscure prefixes, but these are commonly used in the math world, and it's essential to know most of them. Especially if you are taking at test and the question reads:
Select One: Is a quadrilateral considered to be (1) a regular polygon or (2) a pentathlon?
You might have read about OVERACHIEVING, PRECOCIOUS PRODIGIES, those brilliant folk whose math ability TRANSCENDS that of UNDERACHIEVERS. Notice all the prefixes?
Unlike the previous list of prefixes, the following group deals with position and order rather than numerical or calculation terms. Nevertheless, these are commonly used mathematics prefixes too.
This post is about pre-fixes, those short letter combinations that appear in front of other (math) words.
| Prefix | Meaning | Example |
| bi- | two | bicycle |
| centi- | one hundred | centimeter, century |
| dec- | ten | decade |
| deci- | one-tenth | decimeter |
| equi- | equal ("in the middle") | equidistant, equiangular |
| femto- | 10⁻¹⁵ or 0.000000000000001 | femtocell phone transmitter (Danish femten 15) |
| giga- | 10⁹ or 1,000,000,000 | gigabytes |
| hemi- | half a sphere | hemisphere, Chrysler HEMI |
| hex- | six | hexagon, hex wrench |
| kilo- | 10³ or 1,000 | kilometer |
| mega- | 10⁶ or 1,000,000 ("big") | megabytes, "it's a mega-project" |
That's enough - I think you get the idea. Of course there are many more obscure prefixes, but these are commonly used in the math world, and it's essential to know most of them. Especially if you are taking at test and the question reads:
Select One: Is a quadrilateral considered to be (1) a regular polygon or (2) a pentathlon?
You might have read about OVERACHIEVING, PRECOCIOUS PRODIGIES, those brilliant folk whose math ability TRANSCENDS that of UNDERACHIEVERS. Notice all the prefixes?
Unlike the previous list of prefixes, the following group deals with position and order rather than numerical or calculation terms. Nevertheless, these are commonly used mathematics prefixes too.
| Prefix | Meaning | Example |
| circum- | around | circumference, circumnavigate (the middle) |
| inter- | between | intersection, international |
| over- | above, upper, excessive | overconfident |
| pre- | ahead, before in line, first in order | prelude, precocious |
| pro- | favoring, motion forward, before its time | propulsion, prodigy |
| trans- | across, beyond | transatlantic, translate, transcend |
| under- | below, behind | underachievers, underarm |
Friday, October 21, 2011
Math is
Math is more. Math is new. Math is fun. Math is you.
Math is a language for encoding and decoding information so it can be shared.
Math is a language of counting, measurement, shapes and calculation.
Math is a language with precise definitions and specialized terms.
Today I am speaking in green. Everyone else's words are black. I've been reading up on what math is all about. Since this blog is about "using the math we learned as kids later when we grow up", these quotes are right up my alley:
Math is hard ("Math Class is Tough" says Barbie).
Math is the study of quantity, space, structure, and change.
Math is problem solving - finding a path to a solution via synthesizing information; applying creative, insightful thinking; looking deeply into a problem and understanding it on a different level.
Arithmetic's appeal to infants is self-evident. Adult life often involves accepting illogical compromises, but children prefer to be logical. If 'houses' is the plural of 'house', then 'mouses' should be the plural of 'mouse' - but it is not. Numbers do not play these language tricks on us; they are reliable. Children who delight in logic love arithmetic. W. W. Sawyer
Mathematicians, like musicians, are notoriously precocious and self-propelled.
Math is a brutal, unforgiving, impersonal, and unusually individualistic activity, yet educators are compelled to promote warm, nurturing classroom environments full of group discussions!
Math can be better understood and enjoyed if it is taught like physics - as a laboratory subject. Students who enter math classrooms expecting to see only a whiteboard would find themselves surrounded by gadgets of every kind. W. W. Sawyer
Mathematical reality lies outside us; our function is to discover or observe it, and the theorems which we prove, and the reports of our 'creations', are simply our notes of our observations of this reality. G. H. Hardy
Classical math = the real world: arithmetic = counting and measurement, algebra = truths about calculations, geometry and trigonometry = sizes and shapes of objects, calculus = velocities of moving objects, etc.
Mathematics first arose in purely practical questions; arithmetic in connection with trade, the gathering of taxes, the reckoning of the calendar; geometry in connection with building and land-surveying...
Mathematical innovation after the Dark Ages was not that people got smarter all of a sudden. No, they improved the User Interface by switching to Arabic numerals (which have a much better user experience than Roman Numerals no matter what the Superbowl tries to tell you).
If math was doled out to you in a standardized, unimaginative, incomprehensible manner, you will find it hard to imagine mathematics as a subject of fascination; you will regard it as something done to children, rather than by them.
I hope nobody will draft regulations to forbid any of my pupils from choosing mathematics, more mathematics, still more mathematics, advanced mathematics and very advanced mathematics - if that is what he or she wants to do.
Math is like a foreign language. When you study a language, you know going in that you won’t understand some of the words. In math, you think you know the words. But the words aren't the same. Set, prove, hypothesis, term, and solution don't mean what they do in ordinary English.
Math is about more than abstract equations, slide rulers and calculators: It rules the world.
Higher Math may be dangerous. Warren Buffett
Modern Math is completely useless. Morris Kline
Math is the queen of sciences. Karl Fredreich Gauss
Math is the language with which God has written the universe. Galileo
Thursday, October 20, 2011
Take the money and retire
Today in the Excel Math blog we will choose the 3rd and last topic that focuses on the elementary math implications of the word retire. We've already looked at getting new tires for your car, and throwing out 3 batters in a row. Which will be next?
LIFE CYCLE
Before we can focus on the retiring part, we need to look at the normal money cycle. This is completely separate from political discussions of "the government just prints extra money when they need it". Let's assume the money supply is staying constant and we are not in a time of expansion or contraction of the economy.
Here is the life cycle of paper money:
RETIRING
The Treasury decided in 1969 to retire all bills with value greater than $100. At that time we were using $500, $1000, $5000 and $10,000 bills, even though these bills had not been reprinted since 1945 (the end of WW II). How did this retirement happen?
I can think of these different contributions to the subtraction process:
As we watch this process unfold, we also have to print new bills of other denominations (or mint dollar coins) to make up for the missing "liquidity value" of the notes we've retired.
PREDICTION
Here are the print quantities for bills in the past 6 years. Read the table carefully. Each group of colored columns represents the quantity of one size of bills printed over a 7-year period.
NOTE: Lots of $100s were printed in 2010, as the Bureau introduced a new $100 bill design. Total value of the notes printed in 2010 was about $975 million, at a cost of 9.6¢ per note.
Using the data in this table, which of the 7 denominations of bills do you predict the Treasury might be likely to retire (discontinue) next?
- retire - stop performing one's work or withdraw from one's position
- retire - back away, retreat
- retire - go to bed
- retire - take out of circulation or recall (as in paper currency, bonds, etc)
- retire - strike out or throw out (in baseball)
- re-tire - put new tires on your car
LIFE CYCLE
Before we can focus on the retiring part, we need to look at the normal money cycle. This is completely separate from political discussions of "the government just prints extra money when they need it". Let's assume the money supply is staying constant and we are not in a time of expansion or contraction of the economy.
Here is the life cycle of paper money:
- United States Treasury's Bureau of Engraving and Printing creates plates and prints bills.
- The 12 regional Federal Reserve Banks order bills using as collateral gold, certificates and bonds they have on deposit with the government.
- Each Fed bank keeps an inventory of all bill denominations on hand.
- When commercial banks need cash, they order it from their local Fed, which delivers it to them.
- 50% or more bills are outside the USA, so other agents do this for overseas banks
- Banks pay for the cash using reserve accounts they've established with their Fed.
- Banks put the money into ATM machines and their cash drawers.
- Customers withdraw the money and take it away in pockets and purses.
- People buy things from each other and stores, and the cash goes in all directions.
- When the "buying season" (weekend, holiday) is over the banks end up with too much cash.
- Banks send the excess cash back to the Fed.
- Fed Banks inspect, wash, destroy and/or order new bills depending upon their condition.
- Bills last from 1.5 to 7.5 years, depending upon denomination
- The NY Fed processes 19-20 million notes daily, and destroys 5 million of them
- Counterfeit notes are marked and sent to the Secret Service, which tracks counterfeiters
- Companies making money changing/counting machines can get samples of good and bad (fake) notes
- The Fed banks pay the Treasury the 5-10¢ that each bill costs to print.
- There are roughly 830 billion dollars worth of notes in circulation at any time.
RETIRING
The Treasury decided in 1969 to retire all bills with value greater than $100. At that time we were using $500, $1000, $5000 and $10,000 bills, even though these bills had not been reprinted since 1945 (the end of WW II). How did this retirement happen?
I can think of these different contributions to the subtraction process:
- some notes were damaged
- some notes were lost
- some notes were outside the USA
- some notes are still in existence in the hands of collectors
- some notes were turned in - owners were given equal value in smaller notes.
As we watch this process unfold, we also have to print new bills of other denominations (or mint dollar coins) to make up for the missing "liquidity value" of the notes we've retired.
PREDICTION
Here are the print quantities for bills in the past 6 years. Read the table carefully. Each group of colored columns represents the quantity of one size of bills printed over a 7-year period.
NOTE: Lots of $100s were printed in 2010, as the Bureau introduced a new $100 bill design. Total value of the notes printed in 2010 was about $975 million, at a cost of 9.6¢ per note.
Using the data in this table, which of the 7 denominations of bills do you predict the Treasury might be likely to retire (discontinue) next?
Wednesday, October 19, 2011
Retiring the Side
Yesterday in this math blog I listed some definitions for retire.
NOTE: I have found that men who carefully avoid math in every other realm of life don't seem to notice that sports statistics involve math ...
When three players are called out, the side is retired and the other team goes to bat. Ideally, these players would be struck out at the plate rather than getting on base. A pitcher who can strike out lots of batters and retire the side without giving batters a chance to score is very valuable to any team.
I found a website called Retire The Side™. But I don't think that precludes me from investigating the term myself. So let's move on and see what we can learn.
The most strike-outs recorded in a nine-inning major league game are:
As I did some of my research on this subject, I learned of a minor league baseball pitcher, Ron Necciai, who threw 27 strike-outs in a game. He retired the side 9 times (although he also hit a batter and walked one). WOW! Now that's pitching. Amazingly, four of those strike-outs came in the last inning.
I thought, What?! How could he get 4 strike-outs in one inning? Doesn't the side get retired after 3? After re-reading the article a couple times, I understood.
Interested? Or do you know the loophole already?
This doesn't happen very often in a nine-inning game - here's the list. A few minor league pitchers have pitched five strike-outs to retire the side, along with Phil Niekro who did it in a major league exhibition game.
I learned that Tim Hudson (a pitcher for the Braves) was recently able to get 3 men out and retire the side with just 4 pitches.
This kind of baseball information (and lots more) can be captured and displayed on baseball scorecards. Go here to see a fantastic scorecard and here to see another one. If you want to purchase baseball statistics, you can go to Baseball Info Solutions. Tell them you like math and you want some numbers to practice with ...
- retire - stop performing one's work or withdraw from one's position
- retire - back away, retreat
- retire - go to bed
- retire - take out of circulation or recall (as in paper currency, bonds, etc)
- retire - strike out or throw out (in baseball)
- re-tire - put new tires on your car
NOTE: I have found that men who carefully avoid math in every other realm of life don't seem to notice that sports statistics involve math ...
When three players are called out, the side is retired and the other team goes to bat. Ideally, these players would be struck out at the plate rather than getting on base. A pitcher who can strike out lots of batters and retire the side without giving batters a chance to score is very valuable to any team.
I found a website called Retire The Side™. But I don't think that precludes me from investigating the term myself. So let's move on and see what we can learn.
The most strike-outs recorded in a nine-inning major league game are:
- 20 (3 times)
- 19 (8 times)
- 18 (13 times)
- 21 (once)
- 20 (once)
- 19 (4 times)
- 18 (3 times)
As I did some of my research on this subject, I learned of a minor league baseball pitcher, Ron Necciai, who threw 27 strike-outs in a game. He retired the side 9 times (although he also hit a batter and walked one). WOW! Now that's pitching. Amazingly, four of those strike-outs came in the last inning.
I thought, What?! How could he get 4 strike-outs in one inning? Doesn't the side get retired after 3? After re-reading the article a couple times, I understood.
Interested? Or do you know the loophole already?
- If a batter is thrown out on strikes AND
- the catcher drops the third strike pitch AND
- there is no one on first (so it's open) AND
- the batter gets to first base before the ball does
- then the pitcher is awarded a strike-out AND the batter gets a base at the same time
This doesn't happen very often in a nine-inning game - here's the list. A few minor league pitchers have pitched five strike-outs to retire the side, along with Phil Niekro who did it in a major league exhibition game.
I learned that Tim Hudson (a pitcher for the Braves) was recently able to get 3 men out and retire the side with just 4 pitches.
This kind of baseball information (and lots more) can be captured and displayed on baseball scorecards. Go here to see a fantastic scorecard and here to see another one. If you want to purchase baseball statistics, you can go to Baseball Info Solutions. Tell them you like math and you want some numbers to practice with ...
Tuesday, October 18, 2011
The math of re-tiring?
Today in the math blog I would like to consider some math related to re-tiring. What do I mean? Is it:
TIRES
I researched types, sizes and prices on all sorts of tires this morning. Here's what I found:
Although these are all tires, it's apparent that we cannot compare them directly. Even within each category, the range is tremendous. I divided the weight by the dollars and came up with this:
This is not way to choose which tires to buy. The "value per unit" is not found by comparing the weights! Tire prices are not related to how much rubber you get. In fact, with bicycles, it's the other way around - the price is related to how little weight you get.
The best way to choose a tire is to read reviews on national tire websites and then talk to the manager of your local tire, motorcycle or bicycle store.
INSTALLATION
Tires are a nuisance to install. You lift the vehicle, take off the wheel, leave a corner of the vehicle lifted (or motorcycle/bicycle on a stand). Using a tool or machine, you remove the tire from the wheel, put the new one on, inflate the tire, and reinstall it on the vehicle. Very few of us can do this work at home - we must rely on the expertise of a mechanic. In a former job I changed thousands of bicycle tires. I can appreciate the labor involved!
EXTRAS
As if this wasn't enough, we are faced with a barrage of optional-at-extra-cost services associated with the tires and the replacement. We must think about purchasing:
Without a basic understanding of math, how can we even compare bottom-line prices for tires?
We can't! Here's a typical formula that shows how your $100 tire really costs $151.50.
$432 Tires $100 x 4 = $400 x 1.08 (tax) = $432
$ 65 Mount & balance $15 x 4 = 60 x 1.08 = $65
$ 13 Stems $3 x 4 = 12 x 1.08 = $13
$ 16 Disposal fees $4 x 4 = $16
$ 80 Road Hazard warranty 4 x $20 = $80
$606 Cost Per tire = $606 ÷ 4 = $151.50
- retire - stop performing one's work or withdraw from one's position
- retire - back away, retreat
- retire - go to bed
- retire - take out of circulation or recall (as in paper currency, bonds, etc)
- retire - strike out or throw out (in baseball)
- re-tire - put new tires on your car
TIRES
I researched types, sizes and prices on all sorts of tires this morning. Here's what I found:
| Type of tires | Low Price | High Price | Low Weight | High Weight |
| Car & Light Truck | 49 | 742 | 16.0 | 86.0 |
| Motorcycle & Scooter | 34 | 384 | 8.0 | 23.0 |
| Bicycle & Unicycle | 12 | 140 | 0.3 | 2.8 |
Although these are all tires, it's apparent that we cannot compare them directly. Even within each category, the range is tremendous. I divided the weight by the dollars and came up with this:
| Type of tires | Low cost per pound | High cost per pound |
| Car & Light Truck | $0.57 | $46 |
| Motorcycle & Scooter | $1.48 | $48 |
| Bicycle & Unicycle | $4.26 | $467 |
This is not way to choose which tires to buy. The "value per unit" is not found by comparing the weights! Tire prices are not related to how much rubber you get. In fact, with bicycles, it's the other way around - the price is related to how little weight you get.
The best way to choose a tire is to read reviews on national tire websites and then talk to the manager of your local tire, motorcycle or bicycle store.
INSTALLATION
Tires are a nuisance to install. You lift the vehicle, take off the wheel, leave a corner of the vehicle lifted (or motorcycle/bicycle on a stand). Using a tool or machine, you remove the tire from the wheel, put the new one on, inflate the tire, and reinstall it on the vehicle. Very few of us can do this work at home - we must rely on the expertise of a mechanic. In a former job I changed thousands of bicycle tires. I can appreciate the labor involved!
| Type of Tires | Installation Cost | |||||
| Car & Light Truck | $5-25 | |||||
| Motorcycle & Scooter | $10-175 | |||||
| Bicycle & Unicycle | $10-30 |
EXTRAS
As if this wasn't enough, we are faced with a barrage of optional-at-extra-cost services associated with the tires and the replacement. We must think about purchasing:
| Type of Tires | Stem or Tube | Align or True | Balance | HazMat | Weights | Warranty |
| Car & Light Truck | $3-20 | $30-75 | $12-15 | $5-10 | $3-5 | $10-15 |
| Motorcycle & Scooter | $5-30 | $20-50 | $10-20 | $5 | $3-5 | $50 yr |
| Bicycle & Unicycle | $7-30 | $10-30 | 0 | 0 | 0 | 0 |
Without a basic understanding of math, how can we even compare bottom-line prices for tires?
We can't! Here's a typical formula that shows how your $100 tire really costs $151.50.
$432 Tires $100 x 4 = $400 x 1.08 (tax) = $432
$ 65 Mount & balance $15 x 4 = 60 x 1.08 = $65
$ 13 Stems $3 x 4 = 12 x 1.08 = $13
$ 16 Disposal fees $4 x 4 = $16
$ 80 Road Hazard warranty 4 x $20 = $80
$606 Cost Per tire = $606 ÷ 4 = $151.50
Monday, October 17, 2011
Doing it by the numbers
Welcome to the ExcelMathMike blog, where I write about using elementary math in daily life. My "real job" is managing the elementary school math curriculum we publish, which is called (surprise!) Excel Math. I comment on the omnipresence of numbers and math concepts around us.
This post is slightly different today, as I describe the numbers involved in my job, not my real life. I got a letter from a visitor to our Excel Math website. She posed a fascinating and very reasonable question:
Sheesh. You have to remember that to a teacher, Cutting Stuff Out is not always a good thing. Especially when it comes to books.
Could this be a "when did you stop beating your wife?" sort of question?
I wasn't sure, but reasoning that the facts (numbers) were my best defense, I responded like this:
ANSWER: You are getting a similar amount of material, assembled in a different way:
"And so Your Honor, I think the numbers will show that I never actually started beating my wife..."
This post is slightly different today, as I describe the numbers involved in my job, not my real life. I got a letter from a visitor to our Excel Math website. She posed a fascinating and very reasonable question:
QUESTION: I used Excel Math 10 years ago and it had 175 lessons per year. We are looking at Excel Math again, and wondered - what was cut out to bring it down to 155 lessons?
Sheesh. You have to remember that to a teacher, Cutting Stuff Out is not always a good thing. Especially when it comes to books.
Could this be a "when did you stop beating your wife?" sort of question?
I wasn't sure, but reasoning that the facts (numbers) were my best defense, I responded like this:
ANSWER: You are getting a similar amount of material, assembled in a different way:
- All of the Excel Math grades have 155 lessons for 31 weeks of instruction
- We don't provide homework on Fridays, so we created longer, in-depth lessons on Fridays, occupying the Homework space
- Grades 2-6 have 30 tests which formerly appeared on the back of Lesson Sheets but they are now on their own pages
- On the back of 24 tests are "Create A Problems" which assess students' higher-level thinking and reasoning skills; they delve into concepts not easily managed in regular lessons
- We provide 12-24 activities or exercises, introducing kids to measuring, reasoning, graphing, research projects, and so on.
- Glossaries of Math Terms cross-referenced to the lessons in which a word is introduced
- Test Question Concept Tables indicate on which lesson we taught a concept, so you can support students who didn't master that part of the curriculum content
- Projectable Lessons so you can put a lesson up on a screen while you present it to the class
ANSWER: There are other changes:
- We simplified some of the layout of the pages
- We put the answers in different type fonts, so they are easier for the teacher to read
- We "show the work" so teachers can instruct without having to do calculations themselves
- We gave the students a bit more room to write their answers
- We reduced the amount of space used for practicing basic math facts
- We reduced the number of problems teachers were expected to read aloud to the class
- We put in all the modern quarters, nickels, other coins and paper currency
- We tightened up the writing in the Lesson Plans and instructional material
- We improved our description of and teaching of probability
- We adjusted our subject matter content to meet state standards
- We adjusted our "social content" and "political correctness"
- we removed 44 lessons, all repeats on previously-taught subjects
- we added 21 lessons, mostly new topics and/or repeats on other difficult subjects
- we added 36 bonus exercises and activities
- we provided about 7500 total problems (in Lessons, Guided Practice, Homework and Tests)
 |
| Click to enlarge |
"And so Your Honor, I think the numbers will show that I never actually started beating my wife..."
Friday, October 14, 2011
Let's Sort This Out, Part V
We have focused on sorting this week. That means putting data into different arrangements to see if it helps us to analyze and understand what we are working with.
I checked with my spreadsheet documentation to see how it can do sorting. Here's what it can do - notice that your software may vary:
I scanned a Wikipedia page on sorting algorithms which caused me to doze at my desk. If you are a programmer you may wish to check it out. All others, avoid it!
I located a page with tips for solving sorting challenges using Microsoft Excel software (not to be confused with Excel Math, the elementary math curriculum that we publish). Here are some examples:
Do you sort on the numerical values of the colors, their PMS numbers, the alphabetical names of the colors, what? So I went on a search.
Sorting can be one of the most difficult assignments, with many dimensions. We tackle it in Excel Math. Even though they are young, it doesn't mean that what they are learning is easy!
Here's a site that creates color sorting practice worksheets for kindergarteners, try it yourself!
I checked with my spreadsheet documentation to see how it can do sorting. Here's what it can do - notice that your software may vary:
I scanned a Wikipedia page on sorting algorithms which caused me to doze at my desk. If you are a programmer you may wish to check it out. All others, avoid it!
I located a page with tips for solving sorting challenges using Microsoft Excel software (not to be confused with Excel Math, the elementary math curriculum that we publish). Here are some examples:
- Automatically Sorting When you enter text and you want the data to sort itself automatically.
- Ignoring Words when Sorting If you sort movie, book, or product titles, you may want to ignore certain words when sorting.
- Incomplete or Bad Sorting Using sorting tools can jumble the data; how do you repair it?
- Sorting by Colors If you need to sort based on the color of the cell or the data, it's possible!
- Sorting Graphics It seems crazy, but you can sort images that appear in a spreadsheet.
- Sorting Dates by Month Sorting by dates is easy, but it's tricky to sort by months.
- Ascending & Descending Sorting Rules When you sort, programs normally work in a certain pattern or sequence; you need to know this when sorting combined letters and numbers.
Do you sort on the numerical values of the colors, their PMS numbers, the alphabetical names of the colors, what? So I went on a search.

- I found a discussion where someone suggested "You're sorting by redness, then green-ness, then blueness. Probably you're going to have to convert the colors to HSV, and sort by H first (hue) then S (saturation) then V (value/brightness."
- Next guy said "To make the colors transition with the best smoothness, you have to solve a traveling-salesman problem: Find the distance between each two colors (square root of the sum of the squares of the red, green, and blue differences), lay them out in a big table, and find the shortest path that visits each one. The bad news is that this belongs to the hardest known category of computable problems..."
- I found elementary math here "you're trying to map three dimensional values onto one dimension. This results in wave patterns - which frankly is not very satisfactory, as anyone who spent way too much time in kindergarten trying to organize a big box of crayons can tell you!"
- The most useful comment I found said "Colors don't have a canonical linear (fixed) order so the first thing you have to decide is how you want them sorted. If you can't describe how you would do it by hand, you're out of luck when it comes to programming!"
Sorting can be one of the most difficult assignments, with many dimensions. We tackle it in Excel Math. Even though they are young, it doesn't mean that what they are learning is easy!
Here's a site that creates color sorting practice worksheets for kindergarteners, try it yourself!
Thursday, October 13, 2011
Let's Sort This Out, Part IV
I like to watch detective shows when I am not creating elementary math curriculum. I prefer Columbo, Rockford, Hawaii 5-O, Sherlock Holmes, Lovejoy, Murder She Wrote, and similar adventure / mystery stories.
Why do I bring up my detective interest in a series about sorting data?
Because in any detective show there are potential suspects that the detective must discover, question and then eliminate or pursue. Some people answer his questions truthfully. Others avoid, evade, mislead or obstruct his investigation. What must the detective do to solve the case?
A detective must sort out the liars. Find the deceptive, law-breaking people. Then Book 'Em.
In math, we have a similar task. We must sort the outliers.
What do you mean by that? you ask.
An outlier is an data point that is markedly different from the majority of our samples. We don't have a precise mathematical definition of an outlier; we have to make those decision ourselves. But you'll know one when you see one, as I outline the process of outing the outliers.
Let's look at the data from our 25 countries. [click on either chart to enlarge it]
First I sorted our countries by population. The average population is shown in by a line in RED. It's in BLUE when we exclude China, and in GREEN when we exclude the top two and bottom two samples. The average population is probably about 7.5 million.
Now I have resorted the data by area in square kilometers. The average area is shown in RED. It's in BLUE when we exclude China, and in GREEN when we exclude the top two and bottom two samples. The average area is probably about 215,000 sq km.
Outliers show up most clearly when you plot data points on a graph. Here's the same data plotted on charts. See the obvious outlier(s), outlined in red?
If people living in China hadn't visited this site recently, our outliers would be defined differently. Let's take a look. Here are the new outliers, in green.
This looks dramatically different. The outliers are Burma (population) and Libya (area), and the scales on our graph cover a much smaller range of numbers.
We'll finish our sorting tomorrow.
Why do I bring up my detective interest in a series about sorting data?
Because in any detective show there are potential suspects that the detective must discover, question and then eliminate or pursue. Some people answer his questions truthfully. Others avoid, evade, mislead or obstruct his investigation. What must the detective do to solve the case?
A detective must sort out the liars. Find the deceptive, law-breaking people. Then Book 'Em.
In math, we have a similar task. We must sort the outliers.
What do you mean by that? you ask.
An outlier is an data point that is markedly different from the majority of our samples. We don't have a precise mathematical definition of an outlier; we have to make those decision ourselves. But you'll know one when you see one, as I outline the process of outing the outliers.
Let's look at the data from our 25 countries. [click on either chart to enlarge it]
First I sorted our countries by population. The average population is shown in by a line in RED. It's in BLUE when we exclude China, and in GREEN when we exclude the top two and bottom two samples. The average population is probably about 7.5 million.
Now I have resorted the data by area in square kilometers. The average area is shown in RED. It's in BLUE when we exclude China, and in GREEN when we exclude the top two and bottom two samples. The average area is probably about 215,000 sq km.
Outliers show up most clearly when you plot data points on a graph. Here's the same data plotted on charts. See the obvious outlier(s), outlined in red?
If people living in China hadn't visited this site recently, our outliers would be defined differently. Let's take a look. Here are the new outliers, in green.
This looks dramatically different. The outliers are Burma (population) and Libya (area), and the scales on our graph cover a much smaller range of numbers.
We'll finish our sorting tomorrow.
Wednesday, October 12, 2011
Let's Sort This Out, Part III
This blog is all about using elementary math when you are grown up. This week the subject is sorting data. I have collected, sorted, and studied information about 25 countries from which we have had one or more new visitors.
Here's my data list sorted by Latitude, from lowest to highest. The numbers indicate an angle measured in degrees above or below the equator. The N (or +) in each latitude coordinate means Northern Hemisphere and the S (or -) means Southern Hemisphere.
In this sort, the lowest numbers are closest to the equator (0 parallel) and the highest numbers are closest to the poles (90). Since the numbers are sorted in ascending order, the lowest ones are at the top, and the numbers get larger (ascend) as you go down the list. Confusing, isn't it?
Perhaps sorting alphabetically is less confusing, because when you do an ascending sort, you start with A at the top and go down to Z.
When you sort data on a spreadsheet, you have to be very aware of the numbers. In order to get the sorting to work properly, I had to add 2 leading zeros 00 in front of single-digit coordinates, and 1 leading zero 0 in front of double-digit coordinates. That way all coordinates had 3 digits and sorted properly.
Now back to the analysis of our countries!
There are a couple countries very close to the equator - Papau New Guinea and the Ivory Coast. The northernmost country is the Faroe Islands, and the southernmost is Botswana. We can deduce that by observing the numbers, and we can see it on the map below, where I have plotted the coordinates. [click the map to enlarge it]
What do we learn? When you sort data, unexpected details emerge!
Only 6 of the 25 countries are in the Southern Hemisphere. Why do you suppose there are so few? It appears (after I did some research) that only 10-12% of the population lives in the Southern Hemisphere. As you can see, the Equator line on the map does not go through the middle of my image. If I had evenly presented the map of the earth, you would see lots more water in the Southern Hemisphere.
Most of the world's population live in the Northern Hemisphere. All of Europe, all of North and Central America, all of the Caribbean, the vast majority of Asia and two-thirds of Africa are in the Northern Hemisphere.
No wonder there are more countries in the north ... see what we have learned just by using our elementary math?
Here's my data list sorted by Latitude, from lowest to highest. The numbers indicate an angle measured in degrees above or below the equator. The N (or +) in each latitude coordinate means Northern Hemisphere and the S (or -) means Southern Hemisphere.
 |
| Sorted by Latitude |
In this sort, the lowest numbers are closest to the equator (0 parallel) and the highest numbers are closest to the poles (90). Since the numbers are sorted in ascending order, the lowest ones are at the top, and the numbers get larger (ascend) as you go down the list. Confusing, isn't it?
Perhaps sorting alphabetically is less confusing, because when you do an ascending sort, you start with A at the top and go down to Z.
When you sort data on a spreadsheet, you have to be very aware of the numbers. In order to get the sorting to work properly, I had to add 2 leading zeros 00 in front of single-digit coordinates, and 1 leading zero 0 in front of double-digit coordinates. That way all coordinates had 3 digits and sorted properly.
Now back to the analysis of our countries!
There are a couple countries very close to the equator - Papau New Guinea and the Ivory Coast. The northernmost country is the Faroe Islands, and the southernmost is Botswana. We can deduce that by observing the numbers, and we can see it on the map below, where I have plotted the coordinates. [click the map to enlarge it]
What do we learn? When you sort data, unexpected details emerge!
Only 6 of the 25 countries are in the Southern Hemisphere. Why do you suppose there are so few? It appears (after I did some research) that only 10-12% of the population lives in the Southern Hemisphere. As you can see, the Equator line on the map does not go through the middle of my image. If I had evenly presented the map of the earth, you would see lots more water in the Southern Hemisphere.
Most of the world's population live in the Northern Hemisphere. All of Europe, all of North and Central America, all of the Caribbean, the vast majority of Asia and two-thirds of Africa are in the Northern Hemisphere.
No wonder there are more countries in the north ... see what we have learned just by using our elementary math?
Tuesday, October 11, 2011
Let's Sort This Out, Part II
Yesterday we started a series on sorting data.
I selected the most recent 25 countries visiting this blog and assembled some numerical data, including country, number of visitors, population, area, latitude, longitude and political status. Yesterday we covered population and size. Today we start to define the location of these countries.
You can see below that I have sorted the list by the numerical value of the Longitude coordinates (sometimes called meridian). That means degrees of rotation on the earth's surface, east or west from the Prime Meridian. This line passes through the Royal Observatory in Greenwich, England (near London). [click on the map to enlarge it]
Countries with the lowest Longitude numbers are closest to England
The highest numbers are on the other side of the earth, in the Pacific Ocean. If the data doesn't show E or W, it must show degrees + (east) or - (west). You need both the degrees and a directional reference to have a Longitude coordinate point or line.
With Latitude and Longitude plus a bit of elementary math, we can tell where a country is located. We can say "Jersey is 49N, 2W". It's up to our listener to figure out that he can't drive West to Bristol, then South Guernsey or Jersey. We don't have to say "Jersey is about 100 miles South of England's southern coastline and about 14 miles West of France, out in the English Channel."
Notice that Guernsey and Jersey appear to be in the same place, according to my rough data in the table, although in reality they are about 20 miles apart. [click the map to enlarge it]
The "round numbers" in my chart are not precise enough for real navigation. To actually find the right island, we need greater precision, such as "the location of the harbor wall on Jersey is 49°11' 00" N and 02°07' 00" W."
The countries with the highest Longitude numbers are out in the Pacific Ocean
Fiji is 8° W of the 180° line and Samoa is 5° degrees E for a total of 13° distance (horizontally). They are 5° apart in latitude (vertically). A line leaving Fiji runs diagonally northwards and eastwards to Samoa. Navigation on the surface of a curved globe takes more skill and math knowledge than we have available today, so I checked Google Maps and learned they are 710 miles apart. [click the map to enlarge it]
All this with only elementary math and a little sorting and studying.
I selected the most recent 25 countries visiting this blog and assembled some numerical data, including country, number of visitors, population, area, latitude, longitude and political status. Yesterday we covered population and size. Today we start to define the location of these countries.
You can see below that I have sorted the list by the numerical value of the Longitude coordinates (sometimes called meridian). That means degrees of rotation on the earth's surface, east or west from the Prime Meridian. This line passes through the Royal Observatory in Greenwich, England (near London). [click on the map to enlarge it]
Countries with the lowest Longitude numbers are closest to England
The highest numbers are on the other side of the earth, in the Pacific Ocean. If the data doesn't show E or W, it must show degrees + (east) or - (west). You need both the degrees and a directional reference to have a Longitude coordinate point or line.
 |
| Sorted By Longitude |
Notice that Guernsey and Jersey appear to be in the same place, according to my rough data in the table, although in reality they are about 20 miles apart. [click the map to enlarge it]
The "round numbers" in my chart are not precise enough for real navigation. To actually find the right island, we need greater precision, such as "the location of the harbor wall on Jersey is 49°11' 00" N and 02°07' 00" W."
The countries with the highest Longitude numbers are out in the Pacific Ocean
Fiji is 8° W of the 180° line and Samoa is 5° degrees E for a total of 13° distance (horizontally). They are 5° apart in latitude (vertically). A line leaving Fiji runs diagonally northwards and eastwards to Samoa. Navigation on the surface of a curved globe takes more skill and math knowledge than we have available today, so I checked Google Maps and learned they are 710 miles apart. [click the map to enlarge it]
Monday, October 10, 2011
Let's Sort This Out, Part I
"Sort this out" is an English-language expression that implies that with a bit of work, we can better understand something. We do this by sifting and shuffling, or mixing things up and waiting for solutions to appear on their own. Our hope is that we will eventually "clear things up" or "get to the bottom of this" or "solve" our problems.
My Morris Dictionary of Word and Phrase Origins tells me that sort comes from the same root as sorcerer, and it's also related to the word fate. People in Roman times would go to a wizard who would let them draw lots to discover their fortune.
Setting aside this lesson in language history, I now want to get to the math. A few days ago, this blog had a special visitor. He or she came from a new country and brought our visitor country count up to 175. You can see the whole list by clicking on the Flag Counter in the left margin.
I thought we would look at the concept of sorting this week, using sample data from the last 25 new countries to come to the Excel Math blog. In this context, sorting means arranging in numerical order from smallest to largest (or the opposite), or in alphabetical order, or in any other logical order we choose (date, color, etc.)
Here's my list of those countries, sorted by the number of visitors from each country:
This statistical data comes from Flag Counter's pages for each country and I typed it into my spreadsheet directly, doing some rounding here and there.
This is the list of countries sorted in ascending order (small to large) by population. I used units of thousands for the population column. That worked well enough for the Caribbean islands, other small countries AND China. China is at the bottom only because I chose to put the smallest populations at the top.
Next, here are the same countries sorted in ascending order by size (area), in square kilometers.
You can see from a quick glance that Macau is half the size of San Marino but it has 18 times the population. It must be crowded there! This fact did not stand out in the previous sorting. Now it has me thinking that I could set up a formula and find the population per sq km for all these countries. But maybe later.
Sifting and Sorting is the kind of analysis that lets us put data into categories (mathematicians tend to call categories sets). We can see common issues that might be based on size, population, or government. For example in both of these sorts we can see that countries of smaller size and/or population tend be part of larger countries.
In Excel Math curriculum, we teach kids to sort in a variety of ways. We'll investigate this technique again tomorrow.
PS - just moments ago, as I was working on this post, a visitor from the Cayman Islands came by, raising the count to 176!
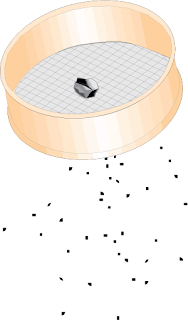 |
| Sifting |
My Morris Dictionary of Word and Phrase Origins tells me that sort comes from the same root as sorcerer, and it's also related to the word fate. People in Roman times would go to a wizard who would let them draw lots to discover their fortune.
Setting aside this lesson in language history, I now want to get to the math. A few days ago, this blog had a special visitor. He or she came from a new country and brought our visitor country count up to 175. You can see the whole list by clicking on the Flag Counter in the left margin.
I thought we would look at the concept of sorting this week, using sample data from the last 25 new countries to come to the Excel Math blog. In this context, sorting means arranging in numerical order from smallest to largest (or the opposite), or in alphabetical order, or in any other logical order we choose (date, color, etc.)
Here's my list of those countries, sorted by the number of visitors from each country:
 |
| Sorted by Number of Visitors to Excel Math Blog, in ascending order |
This is the list of countries sorted in ascending order (small to large) by population. I used units of thousands for the population column. That worked well enough for the Caribbean islands, other small countries AND China. China is at the bottom only because I chose to put the smallest populations at the top.
 |
| Sorted by Population in Thousands, in ascending order |
Next, here are the same countries sorted in ascending order by size (area), in square kilometers.
 |
| Sorted by Area in Square Km, in ascending order |
You can see from a quick glance that Macau is half the size of San Marino but it has 18 times the population. It must be crowded there! This fact did not stand out in the previous sorting. Now it has me thinking that I could set up a formula and find the population per sq km for all these countries. But maybe later.
Sifting and Sorting is the kind of analysis that lets us put data into categories (mathematicians tend to call categories sets). We can see common issues that might be based on size, population, or government. For example in both of these sorts we can see that countries of smaller size and/or population tend be part of larger countries.
In Excel Math curriculum, we teach kids to sort in a variety of ways. We'll investigate this technique again tomorrow.
PS - just moments ago, as I was working on this post, a visitor from the Cayman Islands came by, raising the count to 176!
Subscribe to:
Comments (Atom)









































