Imagine a medical test used to screen people for a disease. We think of the test results being either positive (she has the disease) or negative (he doesn't have the disease). Unfortunately, we can have more than two potential results - we can have four:
- True positive: Sick people are correctly diagnosed as sick
- False positive: Healthy people are incorrectly considered to be sick
- True negative: Healthy people are correctly diagnosed as healthy
- False negative: Sick people are incorrectly considered to be healthy
A high-sensitivity test finds almost all sick people. If you are lucky enough to get a negative result in a high-sensitivity test, it's very likely you don't have the disease.
Example: 100 true positives ÷ (100 true positives + 1 false negative) = 100 ÷ 101 = .99
NOTE: A test which always indicates positive (despite the health of a subject) may have 100% sensitivity but some of its results may be untrue. Sensitivity does not necessarily mean a test is accurate.
Specificity describes the ability of the test to identify negative results (people who DON'T HAVE the disease). Here's a ratio for specificity:
Example: 100 true negatives ÷ (100 true negatives + 5 false positives) = 100 ÷ 105 = .95
NOTE: A test which always indicates negative, (despite the health of a subject) may have 100% specificity, but some of its results may be untrue. Specificity does not necessarily mean a test is accurate.
Sensitivity and Specificity are related to but they are different from Accuracy and Precision.
Accuracy means the degree to which the test results mirror reality. An accurate test gives us the best information about the state of the person's health. Here's one way to represent accuracy:
Ideally, you might say that we want any test to be sensitive, specific, precise, and above all, accurate.
Even math tests?

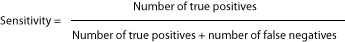



I think you made a mistake on the accuracy one. The numerator should be true positives + true negatives
ReplyDeleteYes, you are correct. Thanks for pointing that out. I'll fix it today. We appreciate your eagle eye. Especially since we want to be precise and accurate on our blog posts, too!
Delete