Aged to Perfection: Numbers

Really? Perfect numbers? How can one number be more or less perfect than another?

Perfect numbers were thought to have important numerological properties by the ancients, and were extensively studied by the Greeks, including Euclid. The ancient Greeks held a great reverence for the mysticism of numbers.

St. Augustine argued that "Six is a number perfect in itself, and not because God created all things in six days; rather the inverse is true; God created all things in six days because the number is perfect.  And it would remain perfect even if the work of the six days did not exist."  (The City of God, Book 11, Chapter 30).

A perfect number is a number where the sum of the number's proper divisors adds up to the number itself. For example:

The first and smallest perfect number is 6. The proper divisors of 6 are 1, 2 and 3. 1 + 2 + 3 = 6 so 6 is a perfect number. (Six is also a factor of 6, but 6 is considered an improper divisor.)

The next perfect number is 28, as its proper divisors are 1, 2, 4, 7, and 14. 1 + 2 + 4 + 7 + 14 = 28 so 28 is also a perfect number. Again, the sum of those integers is 28.
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

8128 is the next perfect number.

Euclid’s theorem: IF (2^k-1) is a prime number THEN 2^{k-1}\times (2^k-1) is a perfect number.

In Euclid's day, these four perfects were all that were known. Incredibly, he saw that for each of these perfects, the formula 2n - 1(2n - 1) produces perfects for the prime n values of 2, 3, 5, 7. Example:

For n=2, 21(22 - 1) = 2(3) = 6.

Notice that 2n-1 is also prime. Euclid brilliantly proved that 2n - 1 (2n - 1) yields an even perfect number when 2n - 1 is a prime number. Note also that not all primes work for n to yield a perfect number.

In the 1700's, Euler expanded on Euclid's formula and proved that it will yield all of the even perfect numbers. Read more at http://trottermath.net/perfect-numbers-et-al/

The first few perfect numbers 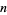 are summarized in the following table together with their corresponding indices :

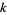1	2	6
2	3	28
3	5	496
4	7	8128
5	13	33550336
6	17	8589869056
7	19	137438691328
8	31	2305843008139952128

Just as we have a scarcity of perfect people, there are not many perfect numbers, which makes them special and worthy of our attention. The third perfect number does not appear until nearly 500; the fourth one is over 8,000; and the fifth one is over 33 million! Read more at http://mathworld.wolfram.com/PerfectNumber.html

In Excel Math, we recognize that perfect numbers are scarce and perfect students perhaps even more so. But all students can develop a love of mathematics and can be given the tools to succeed at math.

Leave a comment below to let us know how you help your students build confidence in math.

Visit our web store to order Student Lesson Sheets (155 lesson sheets plus tests) and a Teacher Edition set of 155 Lessons with brainteasers, teaching suggestions, the answer key, activities, and reproducible manipulatives for each grade level. Excel Math is available for Kindergarten through Grade 6.

Since an entire year of Excel Math curriculum is as low as $11.00 per student, many schools use it as their core curriculum. Other schools find it's a powerful supplement to their adopted curriculum. In both situations, students gain confidence in mathematics as test scores soar.

New to Excel Math? Visit our website at www.excelmath.com for elementary math lessons that really work!